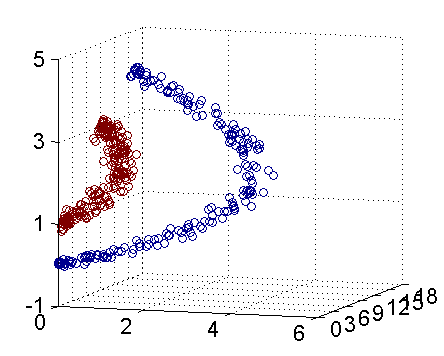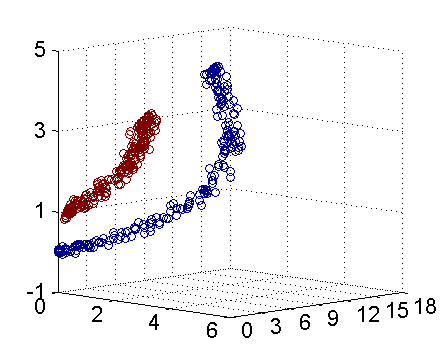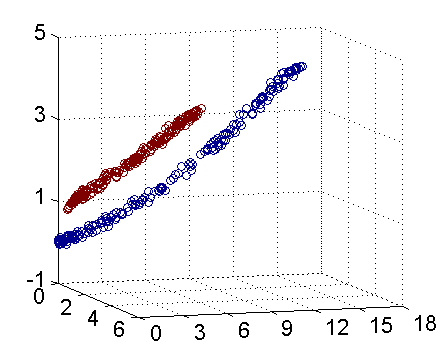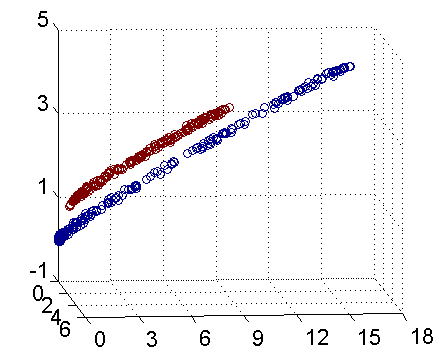
机器学习的算法主要包含监督学习和非监督学习两个大类:
监督学习:简单的说便是,样本集带有属性,需要根据样本集判断新的采样点的属性,常见的knn,svm
非监督学习:与监督学习相反,样本集没有属性信息,需要划分出样本集的分类,常见k-means;
K-means
k-means,k代表将要聚类出的k个cluster,算法流程:
1.随机选出样本集N中k个采样点作为cluster的中心;
2.样板集N中其他采样点选取离自己距离最近的k个cluster center点作为自己的中心点然后
3.通过2我们获得了k个cluster,每个cluster里面有很多点,通过这些点算出每个cluster的中心点(离中心最近的点)
4.重复2,3 直到结果收敛
5.在此算法中比较重要的是距离的计算,根据不同场景使用不同的方式,常用几种距离:
欧几里得距离(Euclidean Distance)
欧氏距离是最常见的距离度量,衡量的是多维空间中各个点之间的绝对距离。公式如下:
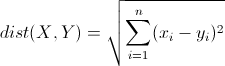
明可夫斯基距离(Minkowski Distance)
明氏距离是欧氏距离的推广,是对多个距离度量公式的概括性的表述。公式如下:
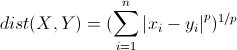
这里的p值是一个变量,当p=2的时候就得到了上面的欧氏距离。
曼哈顿距离(Manhattan Distance)
曼哈顿距离来源于城市区块距离,是将多个维度上的距离进行求和后的结果,即当上面的明氏距离中p=1时得到的距离度量公式,如下:
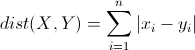
切比雪夫距离(Chebyshev Distance)
切比雪夫距离起源于国际象棋中国王的走法,我们知道国际象棋国王每次只能往周围的8格中走一步,那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步?扩展到多维空间,其实切比雪夫距离就是当p趋向于无穷大时的明氏距离:
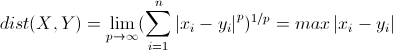
其实上面的曼哈顿距离、欧氏距离和切比雪夫距离都是明可夫斯基距离在特殊条件下的应用。
KnnKnn算法的核心思想便是找出离采样点最近的K个样本点,用这K个样本点来判断采样点的类别,Knn的样本集很大,如果将每个点去运算一次,会造成效率非常低,一般是维护一个最大堆,堆的大小是k,每进来一个样本点动态调整最大堆K;Knn算法比较简单,精确度不及SVM。
SVM
支持向量机(Support Vector Machine,常简称为SVM)是一种监督式学习的方法,可广泛地应用于统计分类以及回归分析。支持向量机属于一般化线性分类器,这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区,因此支持向量机也被称为最大边缘区分类器。支持向量机将向量映射到一个更高维的空间里,在这个空 间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面,分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大,分类器的总误差越小。
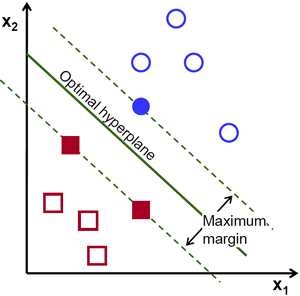
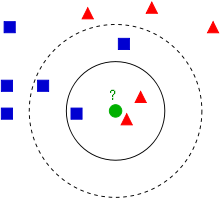
简单的说svm的输入是一些带有属性的样本集,输出是一个平面(高维超平面) ,SVM算法的实质是找出一个能够将某个值最大化的超平面,这个值便是样本集中的点到超平面的距离,所以SVM到最后也转换为求极值问题。
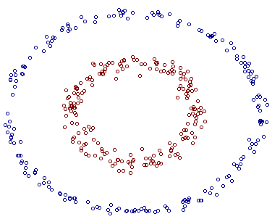
但是会联想到一个问题,如果产生的数据集本来就不是线性可分的改如何处理呢,如下所示:
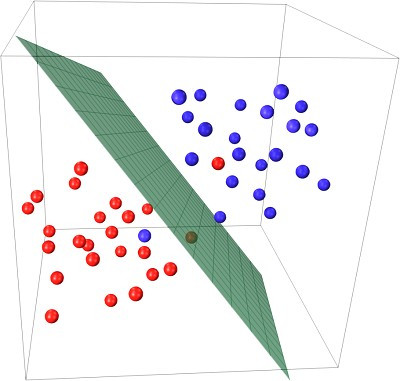
这里就要提到傅里叶变换的思想,在时域不能解决的问题我们会转换到频域来进行处理,既然在当前数据集的维度空间不是线性可分的,将数据集映射到更高维度的空间很可能是线性可分的了,就想圆在二维空间是非线性的但在三维空间就是个平面,映射到高维空间同时带来一个问题:在高维空间上求解一个带约束的极值问题显然比在低维空间上计算量要大得多,这就是所谓的“维数灾难”。于是就引入了“核函数”,核函数的价值在于将特征从低维到高维的转换。
从上图我们可以看出一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用 X1 和 X2 来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:a1X1+a2X21+a3X2+a4X22+a5X1X2+a6=0
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为 Z1=X1, Z2=X21, Z3=X2, Z4=X22, Z5=X1X2,那么显然,上面的方程在新的坐标系下可以写作:
∑i=15aiZi+a6=0
关于新的坐标 Z ,这正是一个超平面 的方程!也就是说,如果我们做一个映射 ϕ:R2→R5 ,将 X 按照上面的规则映射为 Z ,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
最后明显可以看到可以使用一个平面来讲数据集切分